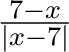Chapter 2: Answers 4 Jack K. Cohen Colorado School of Mines

1. (2.3.16) For x < 7, the quantity x - 7 is negative, so | x - 7| = - (x - 7) = 7 - x. Hence = = 1. As a check:

   LimitTable[(7 - x)/Abs[x - 7], {x, 7, 6, -1}] //TableForm gives:

   6.        1.
   6.9       1.
   6.99      1.
   6.999     1.
   6.9999    1.
   6.99999   1.
   

   (This is our implementation of the recent ``Program of the Week". The last two numerical arguments respectively give the number of table entries and the starting point offset from the limit point (so the table starts with 7 - 1 = 6 in the present case).

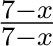2. (2.3.20) = | 4 + x|. For x < - 4 (e.g. x = - 5), the quantity 4 + x is negative, thus | 4 + x| = - (4 + x) and so the limit is -1. Alternately,

   LimitTable[(4 + x)/Sqrt [(4 + x)^2], {x, -4, 6, -1}] //TableForm
   -5.        -1.
   -4.1       -1.
   -4.01      -1.
   -4.001     -1.
   -4.0001    -1.
   -4.00001   -1.
   

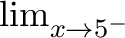3. (2.3.26) x = 5 is the point where the limits don't exist. The function becomes positive large no matter which side we approach 5 from: = = + ∞.